Category Theory for Quantum Natural Language Processing

DisCoPy: a toolkit for computing with string diagrams

Alexis TOUMI

JIQ'22, Paris

QNLP: the meme

QNLP: the recipe

Tree ingredients

Three steps

1. Parse the given text to get a string diagram
2. Map the grammar to a circuit using a functor
3. Tune the parameters to solve a data-driven task

You already use string diagrams without knowing it

• Quantum circuits (see ZX-calculus)
• Tensor networks
• Neural networks
• Concurrent processes
• Electrical circuits
• Logical formulae (see existential graphs)
• The grammar of this sentence is a string diagram!

So what is a string diagram?

A box represents any process with a list of wires as input and output.

A signature is a collection of boxes and wires.

String diagrams can be defined by recursion:

• every box is also a string diagram,
• the identity on a list of wires is a string diagram,
• so is the composition of and
• and the tensor of and .

Cooking recipes are string diagrams!

• Pawel Sobocinski's Graphical Linear Algebra, i.e. linear algebra with all string diagrams and no vectors!

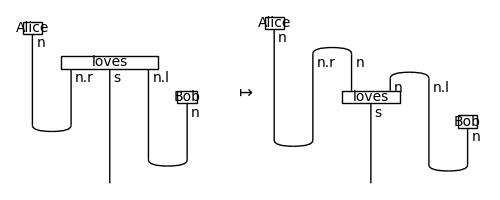
This sentence is a string diagram

• Noam Chomsky, Syntactic Structures (1957)

This sentence is a string diagram

• Joachim Lambek, The mathematics of sentence structure (1958)

• Joachim Lambek, Type grammar revisited (1997)

This Python code is a string diagram

from discopy import Ty, Word, Id, Cup

s, n = Ty('s'), Ty('n')
Alice, loves, Bob = Word('Alice', n), Word('loves', n.r @ s @ n.l), Word('Bob', n)

sentence = Alice @ loves @ Bob >> Cup(n, n.r) @ Id(s) @ Cup(n.l, n)

Monoidal categories

A monoidal category is just a pair of types for objects and arrows with methods:

• dom and cod from arrows to objects,
• id from objects to arrows,
• then and tensor from pairs of arrows to arrows.

For example:

• (Ty, Diagram) is the free monoidal category on a given signature,
• (type, Function), (int, Matrix), (list[int], Tensor), etc.

Monoidal functors

A monoidal functor is just a pair of mappings:

• ob from objects of to objects of ,
• ar from arrows of to arrows of .

For example (Ty, Diagram) (list[int], Tensor)

from discopy.tensor import Functor

F = Functor(ob={s: 1, n: 2},
            ar={Alice: [1, 0], loves: [[0, 1], [1, 0]], Bob: [0, 1]})

assert F(sentence)

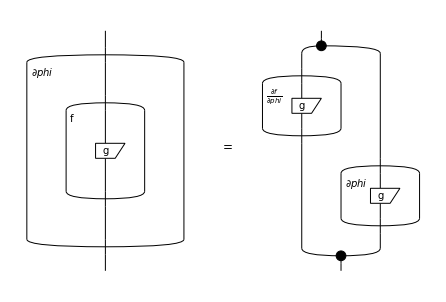
QNLP models

We define a QNLP model as a monoidal functor:

QNLP models

We define a QNLP model as a monoidal functor:

from discopy.quantum import qubit, Ket, H, X, CX, sqrt
from discopy.circuit import Functor

F_ = circuit.Functor(
    ob={s: Ty(), n: qubit},
    ar={Alice: Ket(0), loves: sqrt(2) @ Ket(0, 0) >> H @ X >> CX, Bob: Ket(1)})

assert F_(sentence).eval() == F(sentence)

QNLP models

We define a QNLP model as a parameterised monoidal functor:

Given a dataset with a sentence and its truth value, we want to find the optimal functor :

We call this functorial learning, a new category-theoretic approach to structured machine learning.

Diagrammatic Differentiation for Quantum Machine Learning

joint work with Richie Yeung and Giovanni de Felice

Check it out!

• https://github.com/discopy/discopy
• https://discopy.readthedocs.io
• https://discopy.org