Boxes and signatures

A box represents any process with systems as input and output.

A (monoidal) signature is given by:

• a pair of classes for wires and boxes
• a pair of maps from boxes to lists of wires.

Morphisms of signatures

Given a signature , we write for and with and .

Given two signatures and ,
a morphism is a pair of maps:

• from wire to list of wires
• from box to box

such that for all boxes in the domain we have:

Diagrams: definition

Given a signature , we can define (string) diagrams by recursion:

• every box is also a diagram ,
• the identity on a list of wires is a diagram,
• so is the composition of and
• and the tensor of and .

Diagrams: definition

Diagrams are subject to three axioms.

• Tensor and composition are associative and unital.
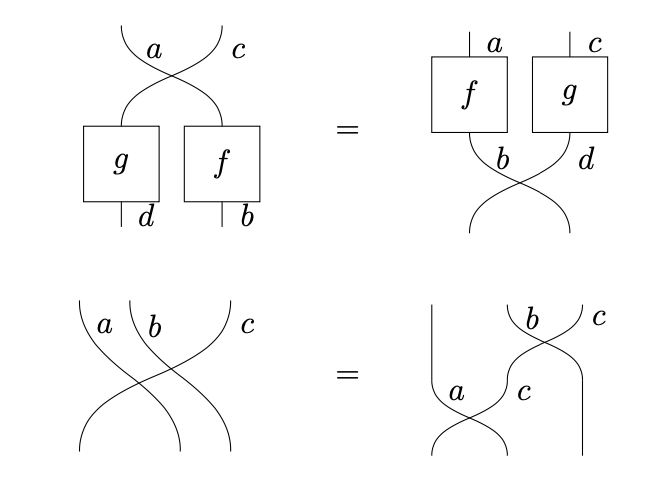
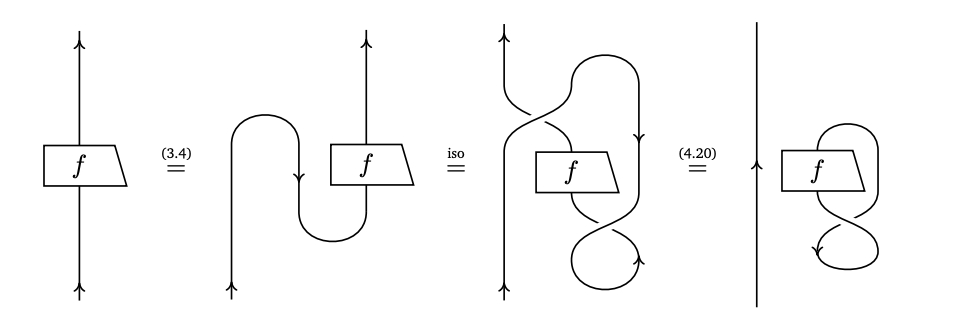
• They satisfy the following naturality equation.

From a signature , we get another signature with wires and diagrams as boxes, and a morphism of signatures .

Diagrams: cooking

Can't be bothered to remember the axioms for diagrams? Your visual cortex has them built in!

• Wires are ingredients.
• Boxes are cooking steps.
• Diagrams are recipes.

In physical terms, naturality means parallel processes are spacelike-separated events.

Diagrams: quantum

Quantum gate sets are signatures!

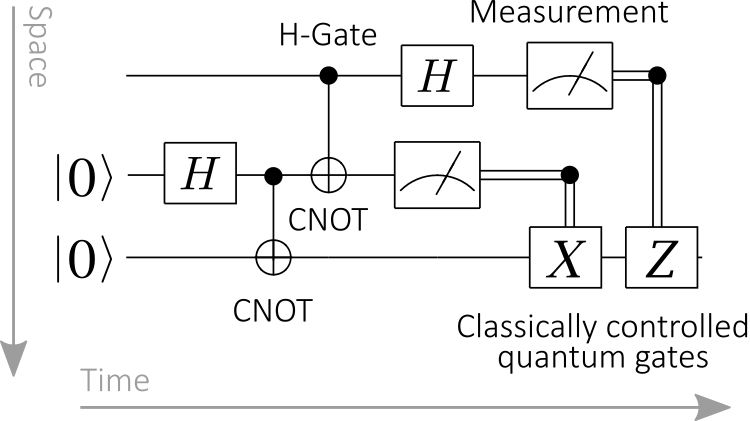
• Wires are bits and qubits.
• Boxes are quantum gates
  and measurements.
• Diagrams are circuits.

Diagrams: grammar

• Chomsky, Syntactic Structures (1957)

Formal grammars are signatures!

• Wires are grammatical types.
• Boxes are grammatical rules.
• Diagrams are grammatical structures.

Diagrams: grammar

• Lambek, The mathematics of sentence structure (1958)

• Joachim Lambek, Type grammar revisited (1997)
• Clark, Sadrzadeh & Coecke, DisCoCat (2008)

Categories: definition

A (strict monoidal) category is a signature with three maps:

such that associativity, unitality and naturality hold. For example:

• : wires and diagrams.
• : sets and functions (with cartesian product as tensor).
• : Hilbert spaces and linear maps (with the tensor product).

Categories: theorem

A (strict monoidal) functor is a morphism of signatures that preserves identity, composition and tensor.

Theorem (Joyal & Street, 1988): is the free monoidal category.

Intuition: The functors are uniquely determined by their image on boxes, i.e. a morphism of signatures .

Categories: grammar

• Montague, English as a formal language (1974)

Natural language semantics as a functor , defined using the lambda calculus and first-order logic.

Categories: grammar

• Coecke, Sadrzadeh & Clark, Mathematical Foundations for a Compositional Distributional Model of Meaning (2010)

DisCoCat models are functors , unifying Dis(tributional) and Co(mpositional) semantics with Cat(egories).

Categories: quantum

• Abramsky & Coecke, Categorical quantum mechanics (2008)
  A categorical semantics of quantum protocols (2004)

The principles of quantum theory as properties of the category .

Categories: symmetric

A category is symmetric if it comes with swaps.

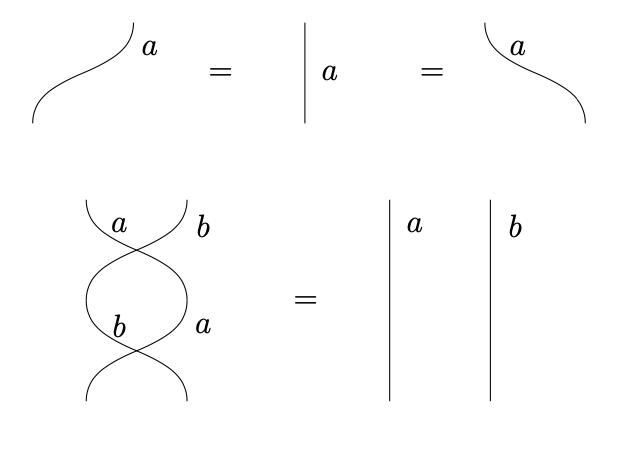
Categories: compact

A symmetric category is compact if it comes with cups and caps.

Entanglement is "the characteristic trait of quantum mechanics".

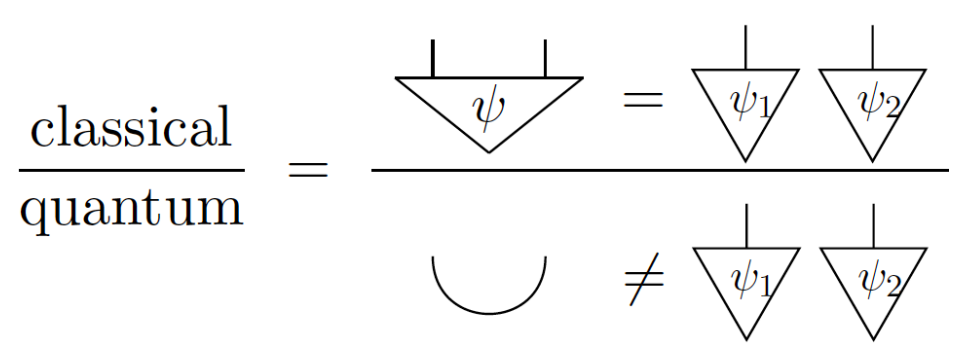
Categories: cartesian

A symmetric category is cartesian if it has copy and discard.

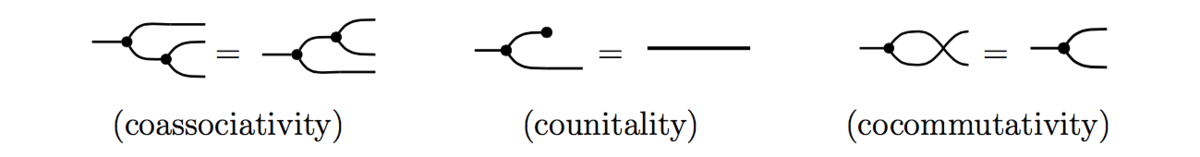
In physical terms, the last equation (again called naturality) is equivalent to causality: the future cannot influence the past.

Categorical no-deleting

Theorem:

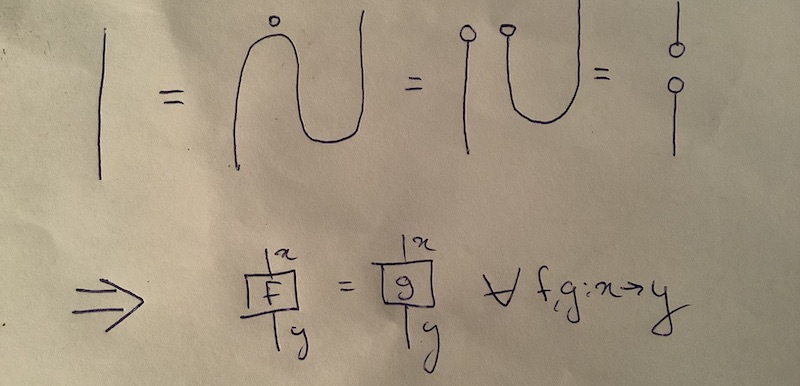
• Abramsky, No-cloning in categorical quantum mechanics (2009)
• Heunen & Vicary, Categories for Quantum Theory (2019)

Categorical no-cloning

Lemma: Suppose a symmetric category has both cups and copy.

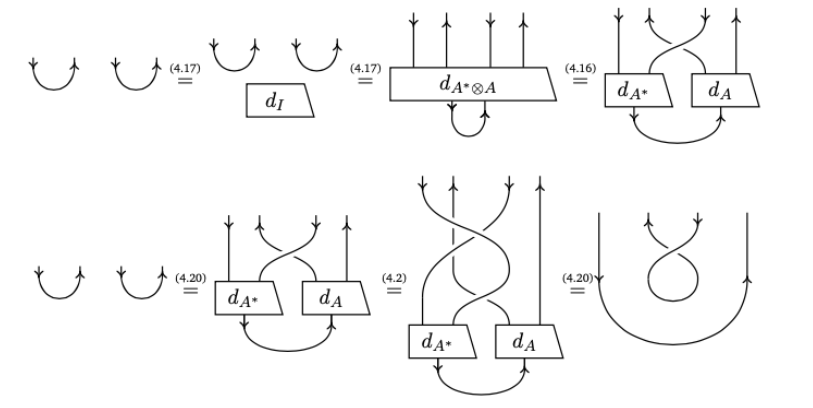
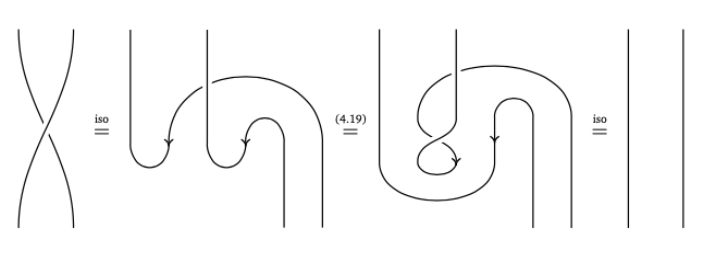
Categorical no-cloning

Theorem:

ZX-calculus

Applications:

• circuit simplification
• circuit compilation
• error correction
• ...
• quantum natural language processing!

https://zxcalculus.com/

QNLP: recipe

Three ingredients

Three steps

1. Parse the text to get a diagram
2. Map it to quantum with a functor
3. Tune parameters to solve NLP tasks (e.g. question answering)

QNLP: definition

We define a QNLP model as a monoidal functor .

• Zeng & Coecke, Quantum algorithms for compositional natural language processing (2016)
• Wiebe et al., Quantum language processing (2019)

QNLP: implementation

We define a QNLP model as a monoidal functor .

from discopy import Ty, Word, Id, Cup
from discopy.circuit import Functor
from discopy.quantum import qubit, Ket, H, X, CX, sqrt

s, n = Ty('s'), Ty('n')
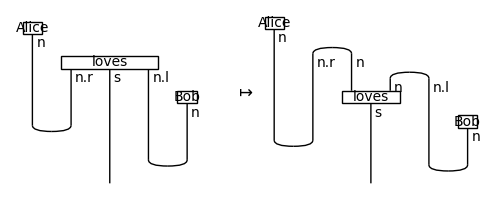
Alice, loves, Bob = Word('Alice', n), Word('loves', n.r @ s @ n.l), Word('Bob', n)

sentence = Alice @ loves @ Bob >> Cup(n, n.r) @ Id(s) @ Cup(n.l, n)

F = circuit.Functor(
    ob={s: Ty(), n: qubit},
    ar={Alice: Ket(0), loves: sqrt(2) @ Ket(0, 0) >> H @ X >> CX, Bob: Ket(1)})

assert F(sentence).eval()

QNLP: training

We define a QNLP model as a parameterised monoidal functor:

Given a dataset with a sentence and its truth value, we want to find the optimal functor :

We call this approach functorial learning, a new category-theoretic approach to structured machine learning.

Diagrammatic Differentiation for Quantum Machine Learning

joint work with Richie Yeung and Giovanni de Felice

DisCoPy: the Python toolkit for computing with string diagrams

https://www.discopy.org