Boxes and signatures

A box represents any process with systems as input and output.

A (monoidal) signature is given by:

• a pair of classes for wires and boxes
• a pair of maps from boxes to lists of wires.

Boxes and signatures

Given two signatures and ,
a morphism is a pair of maps:

• from wire to list of wires
• from box to box

where .

Diagrams: definition

Given a signature , we can define (string) diagrams by recursion:

• every box is also a diagram ,
• the identity on a list of wires is a diagram,
• so is the composition of and
• and the tensor of and .

Diagrams: definition

Diagrams are subject to three axioms.

• Tensor and composition are associative and unital.
• The interchanger ,
  which is equivalent to the following spacelike separation axiom:

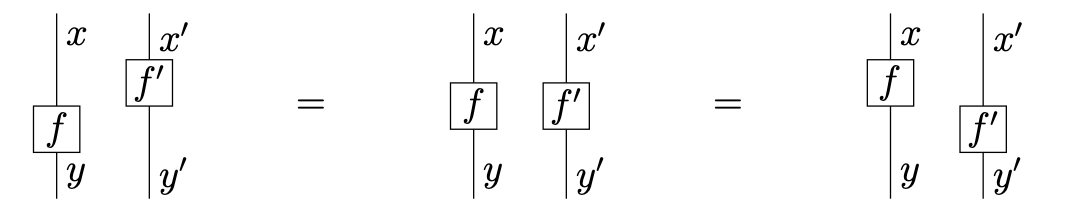
Diagrams: quantum circuits

Quantum gate sets are signatures!

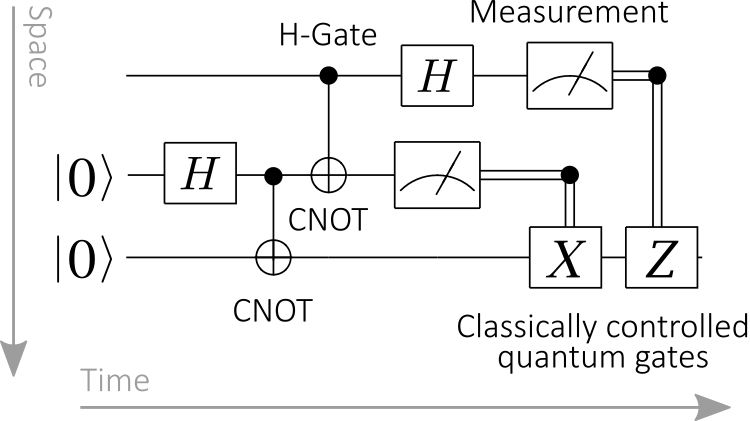
• Wires are bits and qubits.
• Boxes are quantum gates
  and measurements.
• Diagrams are circuits.

Diagrams: grammatical structures

Formal grammars are signatures!

Chomsky: Syntactic Structures (1957)

• Wires are grammatical types.
• Boxes are grammatical rules.
• Diagrams are grammatical structures.

Diagrams: grammatical structures

• Lambek: The mathematics of sentence structure (1958)

• Lambek: Type grammar revisited (1997)
• Clark, Sadrzadeh & Coecke: DisCoCat (2008)

Categories: definition

A (strict monoidal) category is a signature with three maps

such that associativity, unitality and naturality hold.

Functors: theorem

A (strict monoidal) functor is a morphism of signatures that preserves identity, composition and tensor.

Theorem (Joyal & Street, 1988): is the free monoidal category.

Intuition: The functors are uniquely determined by their image on boxes, i.e. a morphism of signatures .

Functors: ZX and ZW calculi

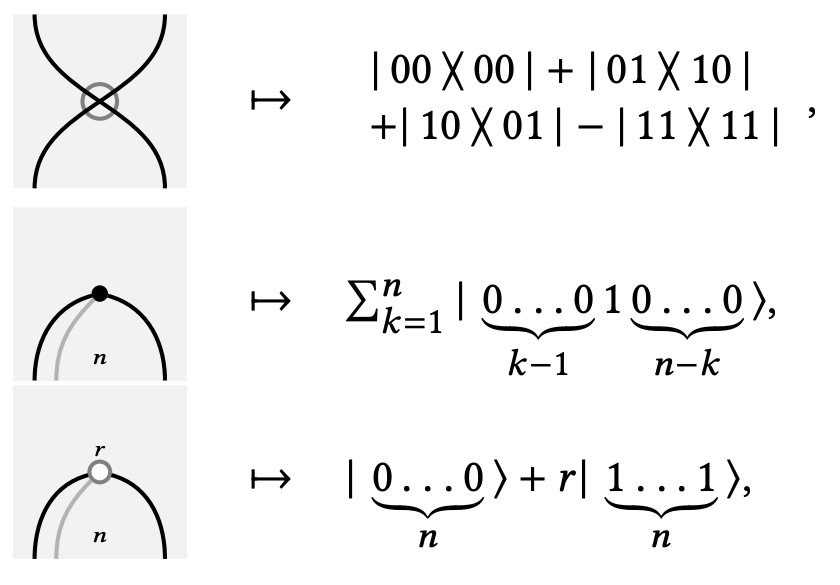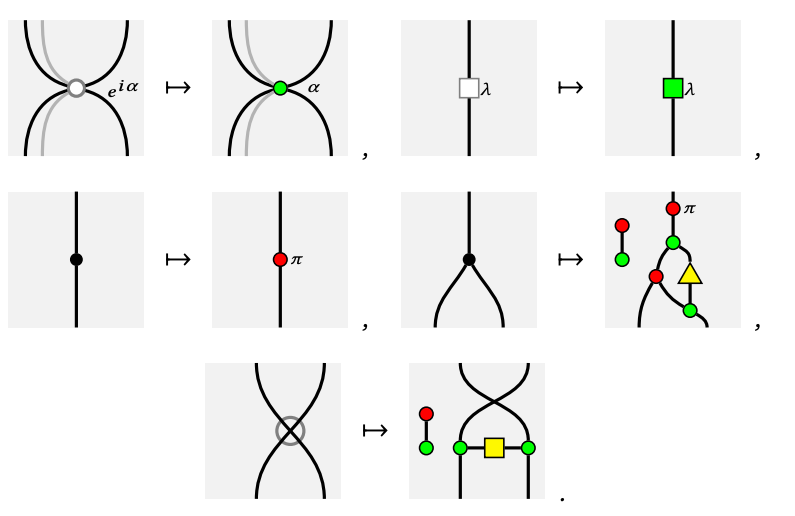Hadzihasanovic, Ng, Wang: Two complete axiomatisations of pure-state qubit quantum computing (2018)

Functors: Montague semantics

• Montague, English as a formal language (1974)

Natural language semantics as a functor , defined using the lambda calculus and first-order logic.

Functors: DisCoCat semantics

• Coecke, Sadrzadeh & Clark, Mathematical Foundations for a Compositional Distributional Model of Meaning (2010)

DisCoCat models are functors , unifying Dis(tributional) and Co(mpositional) semantics with Cat(egories).

Functors: QNLP

A QNLP model is a functor .

• Zeng & Coecke: Quantum algorithms for compositional natural language processing (2016)
• Wiebe et al.: Quantum language processing (2019)
• Meichanetzidis, Toumi, de Felice, Coecke: Grammar-Aware Question-Answering on Quantum Computers (2020)

Frobenius algebras: definition

Coecke, Kissinger: The Compositional Structure of Multipartite Quantum Entanglement (2010)

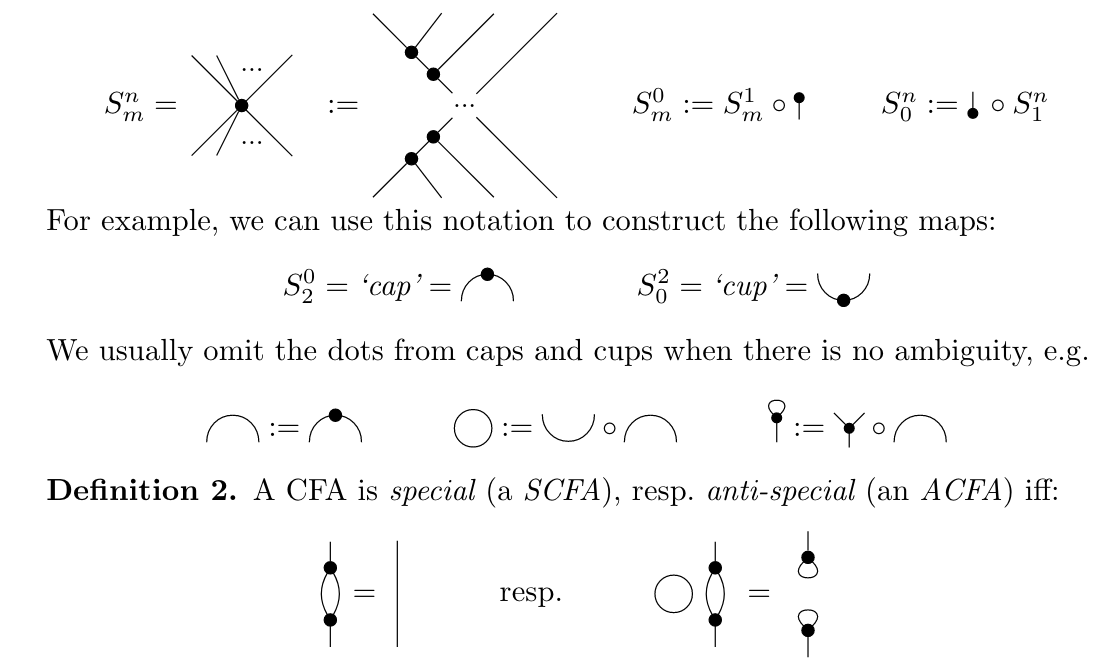
Frobenius algebras: (anti-)special

Frobenius algebras: SLOCC

Dur, Vidal, Cirac:
Three qubits can be entangled in two inequivalent ways. (2000)

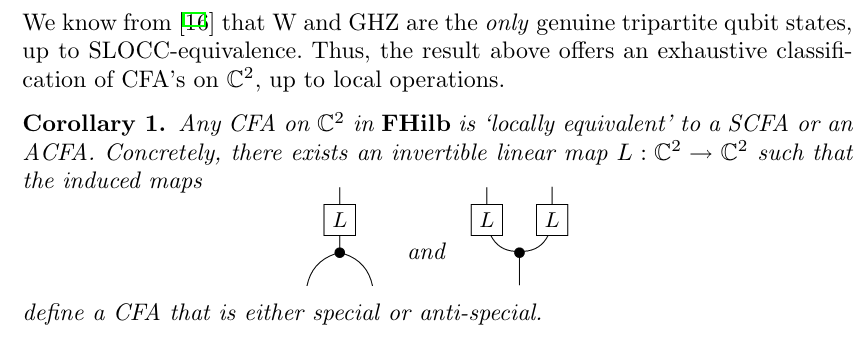
Frobenius algebras: GHZ and W

Frobenius algebras: leader election

If we assume GHZ and W as given, then we can solve
distributed consensus and leader election.

D’Hondt & Panangaden:
The Computational Power of the W and GHZ states (2003)

Frobenius algebras: leader election

Tani, Kobayashi, Matsumoto:
Exact Quantum Algorithms for the Leader Election Problem (2007)

Frobenius algebras: leader election

Tani, Kobayashi, Matsumoto:
Exact Quantum Algorithms for the Leader Election Problem (2007)

Frobenius algebras: leader election

Tani, Kobayashi, Matsumoto:
Exact Quantum Algorithms for the Leader Election Problem (2007)

Frobenius algebras: linguistics

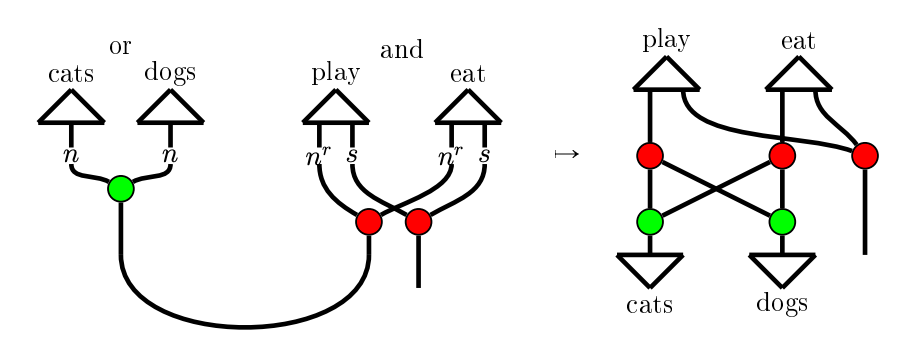
• Sadrzadeh, Clark, Coecke:
  The Frobenius anatomy of word meanings (2013)
• Buet: W-spiders (2017)

Frobenius algebras: linguistics

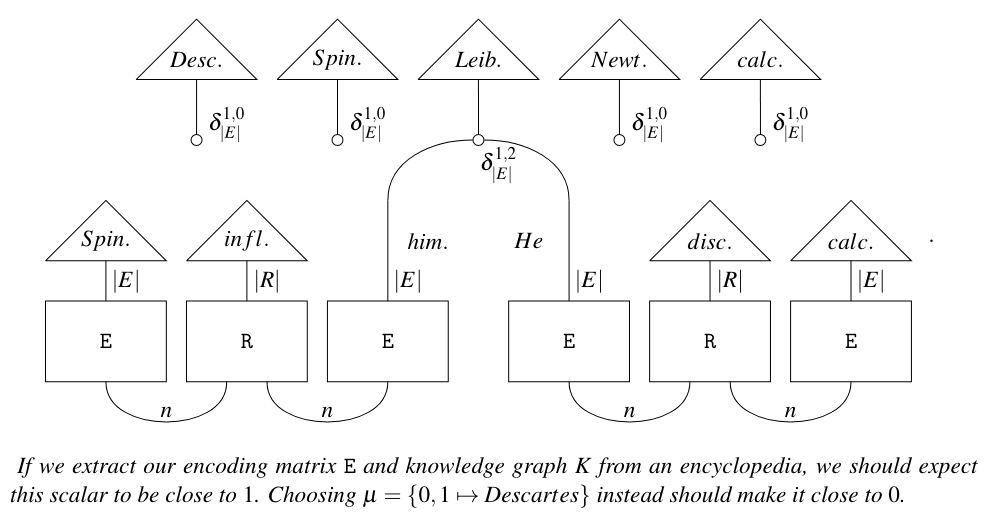
• Coecke, de Felice, Marsden, Toumi: Towards compositional distributional discourse analysis (2018)

Future directions

• Multipartite entanglement as a resource for advantage in QNLP
• Diagrammatic verification for distributed quantum protocols
• Abramsky, Shah: Relating structure and power (2021)
  with game comonads to bound the communication complexity

Thanks!