Boxes and signatures

A box represents any process with systems as input and output.

A (monoidal) signature is given by:

• a pair of classes for wires and boxes
• a pair of maps from boxes to lists of wires.

Boxes and signatures

Given two signatures and ,
a morphism is a pair of maps:

• from wire to list of wires
• from box to box

where .

Diagrams: definition

Given a signature , we can define (string) diagrams by recursion:

• every box is also a diagram ,
• the identity on a list of wires is a diagram,
• so is the composition of and
• and the tensor of and .

Diagrams: definition

Diagrams are subject to three axioms.

• Tensor and composition are associative and unital.
• The interchanger ,
  which is equivalent to the following spacelike separation axiom:

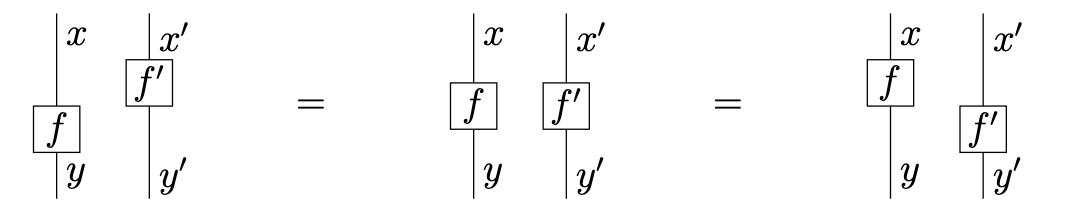
Diagrams: quantum circuits

Quantum gate sets are signatures!

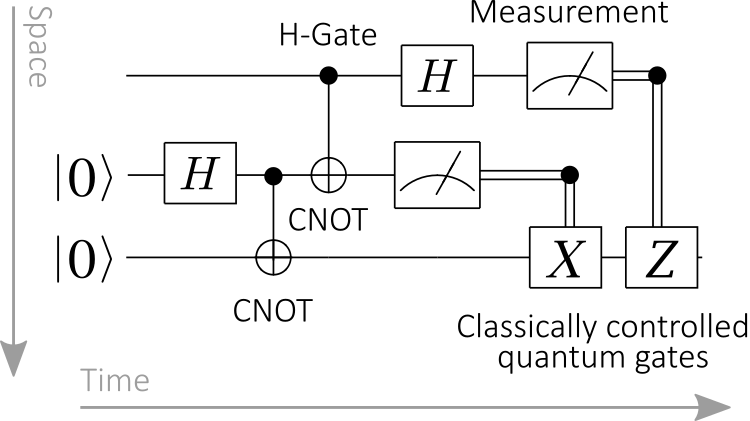
• Wires are bits and qubits.
• Boxes are quantum gates
  and measurements.
• Diagrams are circuits.

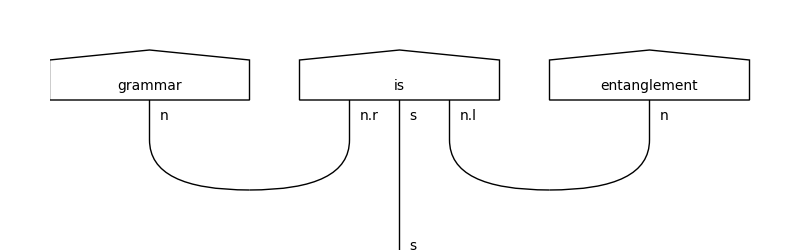
Diagrams: grammatical structures

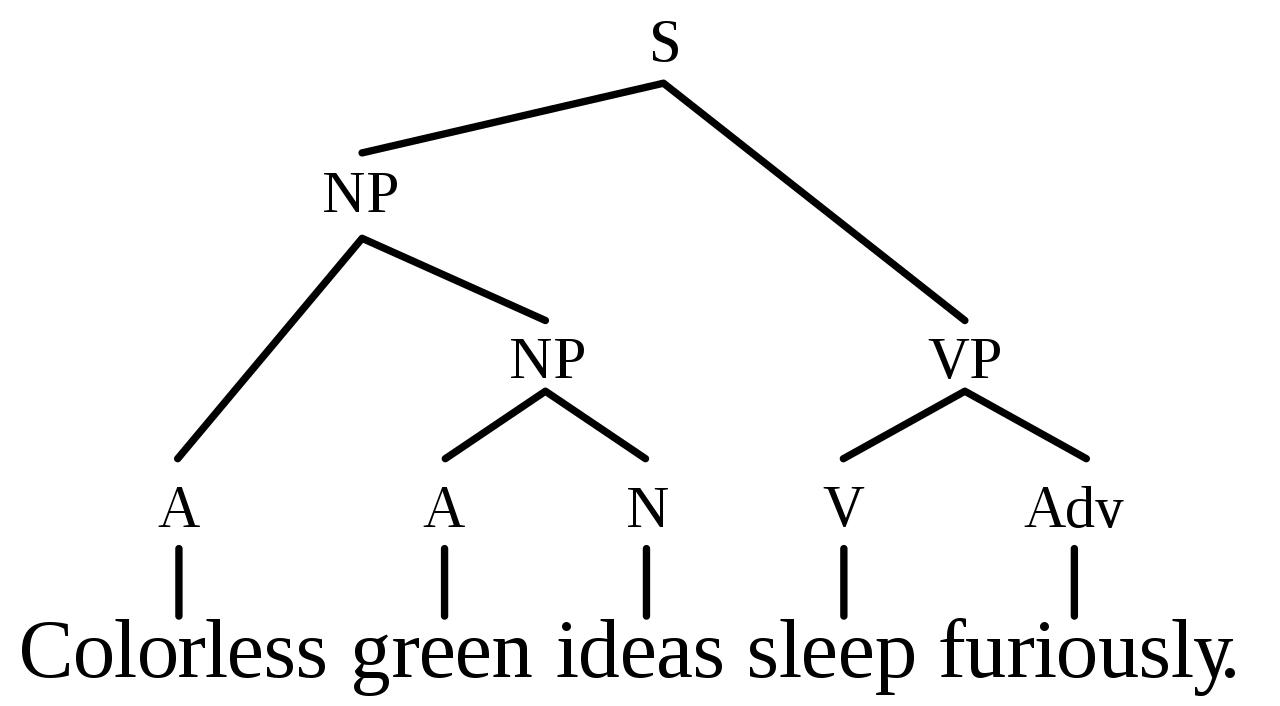
Formal grammars are signatures!

Chomsky: Syntactic Structures (1957)

• Wires are grammatical types.
• Boxes are grammatical rules.
• Diagrams are grammatical structures.

Diagrams: grammatical structures

• Lambek: The mathematics of sentence structure (1958)

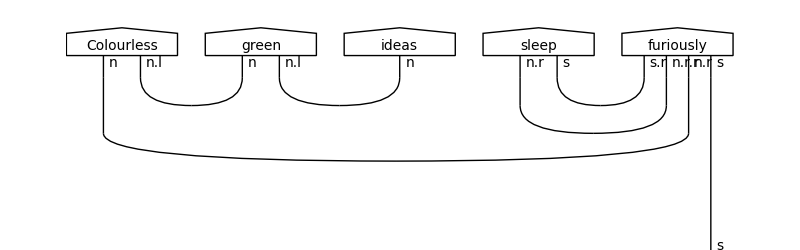
• Lambek: Type grammar revisited (1997)
• Clark, Sadrzadeh & Coecke: DisCoCat (2008)

Categories: definition

A (strict monoidal) category is a signature with three maps

such that associativity, unitality and naturality hold.

Functors: theorem

A (strict monoidal) functor is a morphism of signatures that preserves identity, composition and tensor.

Theorem (Joyal & Street, 1988): is the free monoidal category.

Intuition: The functors are uniquely determined by their image on boxes, i.e. a morphism of signatures .

Functors: Montague semantics

• Montague, English as a formal language (1974)

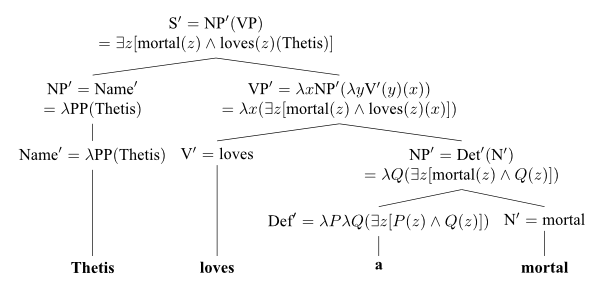
Natural language semantics as a functor , defined using the lambda calculus and first-order logic.

Functors: DisCoCat models

• Coecke, Sadrzadeh & Clark, Mathematical Foundations for a Compositional Distributional Model of Meaning (2010)

DisCoCat models are functors , unifying Dis(tributional) and Co(mpositional) semantics with Cat(egories).

Categorical quantum mechanics

• Abramsky & Coecke, Categorical quantum mechanics (2008)
  A categorical semantics of quantum protocols (2004)

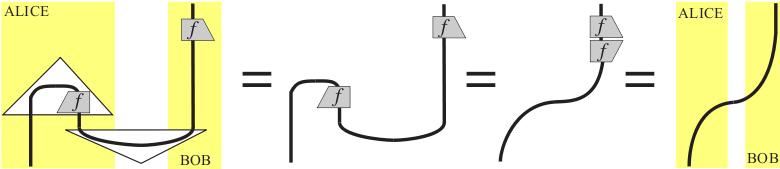
The principles of quantum theory as properties of the category .

QNLP: recipe

Three ingredients

Three steps

1. Parse the text to get a diagram
2. Map it to quantum with a functor
3. Tune parameters to solve NLP tasks (e.g. question answering)

QNLP: definition

We define a QNLP model as a monoidal functor .

• Zeng & Coecke, Quantum algorithms for compositional natural language processing (2016)
• Wiebe et al., Quantum language processing (2019)

QNLP: training

We define a QNLP model as a parameterised monoidal functor:

Given a dataset with a sentence and its truth value, we want to find the optimal functor where

We call this approach functorial learning, a new category-theoretic approach to structured machine learning.

Learning distributed protocols

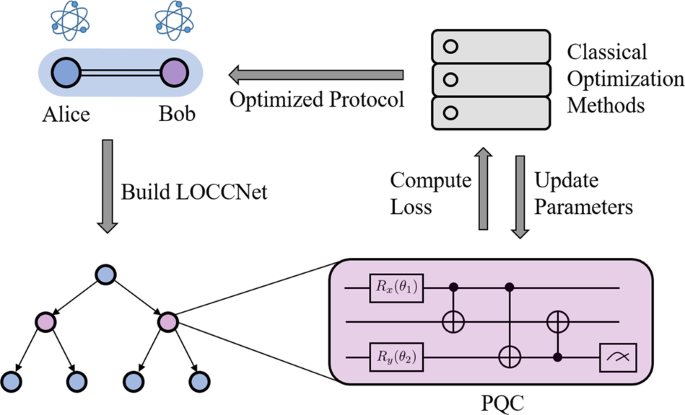
Practical distributed quantum information processing with LOCCNet, Zhao et al. (2021)

Functorial generative modeling

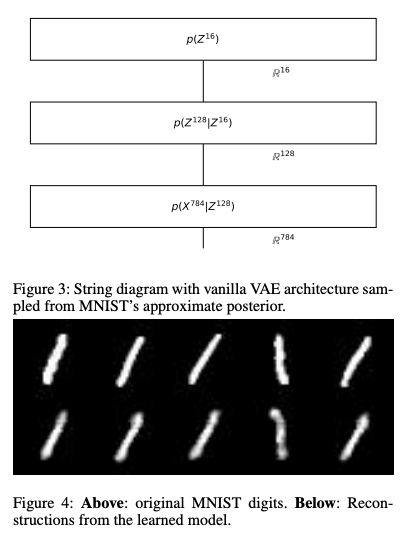
So far, our framework only defines discriminative models .

In order to solve more general tasks (e.g. translation, summarisation) we would need generative models .

Learning a Deep Generative Model like a Program: the Free Category Prior, Sennesh (2020)

Functorial generative modeling

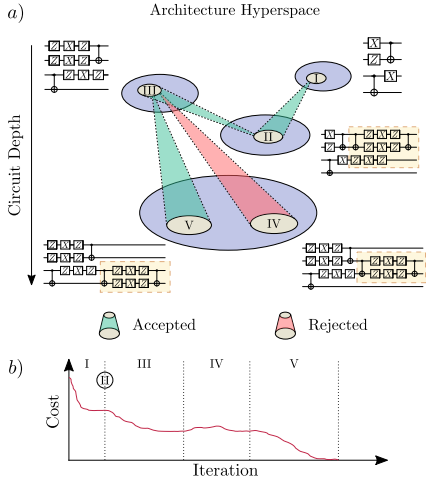
Learning QNLP models requires two steps :

1. combinatorial search for a good ansatz
2. gradient descent to find optimal

A semi-agnostic ansatz with variable structure for quantum machine learning, Bilkis et al. (2021)

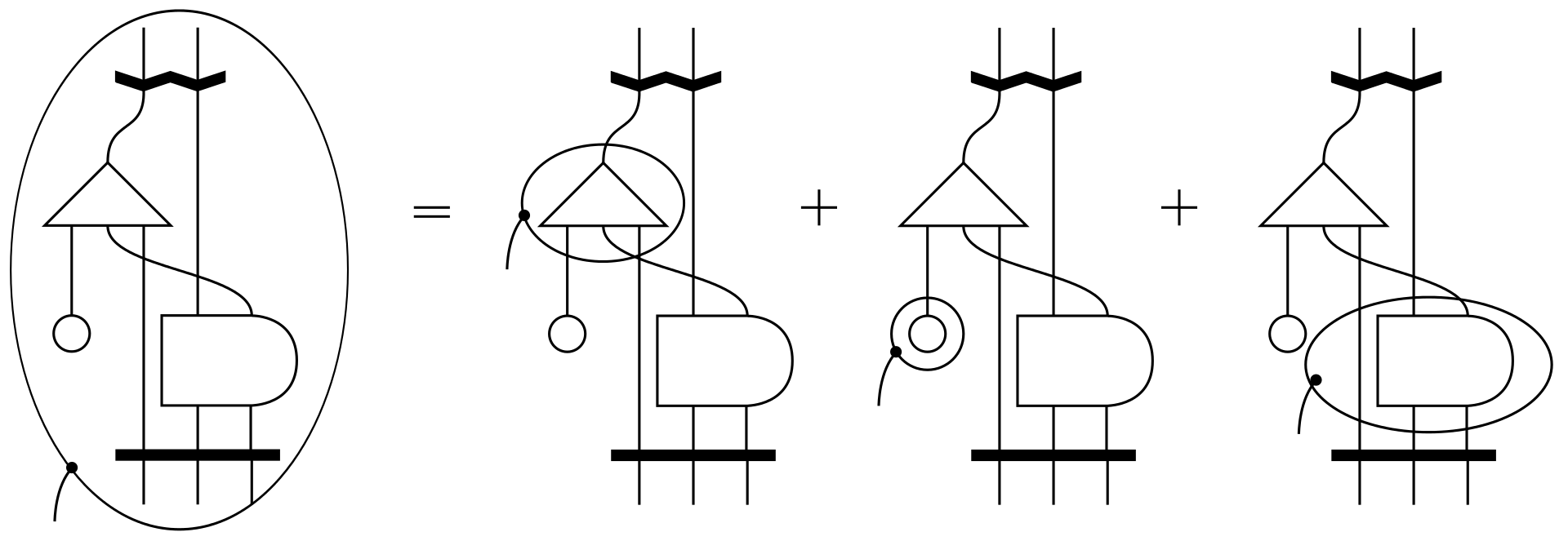
Diagrammatic Differentiation for Quantum Machine Learning

joint work with Richie Yeung and Giovanni de Felice

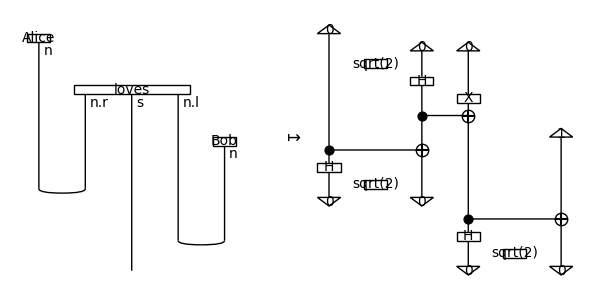
DisCoPy: the Python toolkit for computing with string diagrams

https://discopy.org